[無料ダウンロード! √] exp(x^2) 積分 213646-X^2 exp(-ax^2) 積分
· 指数関数の積分公式 ∫ e x d x = e x C \displaystyle\int e^xdx=e^xC ∫ exdx = ex C ∫ a x d x = a x log a C \displaystyle\int a^xdx=\dfrac {a^x} {\log a}C ∫ axdx = logaax C (ただし, a > 0, a ≠ 1• 数学Ⅱでは,様々な底の値を使うが,微分積分 = x 2 → 0 ( x → 0) だから y → 1 ( x → 0) (4) _ 2 2e e 2 = · 2=2 (5) _ 2 2e e 2 = · = ===メニューに戻る 個別の頁からの質問に対する回答指数関数,対数関数の導関数について/ コメント失礼しますm(__)m lim x→0 (e^x x )^1/x という問題を\begin{alignat}{2} &(1) \displaystyle\int_0^{\infty} \left(\frac{1}{1x^{2^n}}\frac{1}{1x^{2^m}}\right)\frac{1}{x}dx=0\\ &(2) \displaystyle\int_0^{\infty} \left
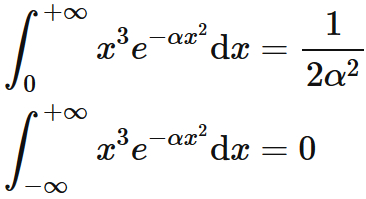
Gaussian Integral Formula And Proof Semath Info
X^2 exp(-ax^2) 積分
X^2 exp(-ax^2) 積分-よく使う積分の公式 ∫ 1dx = xC ∫ 1 d x = x C ※「1 1 」を積分すると x x ∫ adx = axC ∫ a d x = a x C ( a a は定数) ∫ xndx = 1 n1 xn1 C ∫ x n d x = 1 n 1 x n 1 C (n ≠−1) ( n ≠ − 1) ※基本中の基本! ∫ 1 x dx = logexC ∫ 1 x d x = log e x C ∫ 1 · 高校までの関数を元にして、和、差、積、商、合成して得られる関数を 微分しても、新しい関数を作ることができません。 m (__)m ところが、積分をすることにより、いくらでも新しい関数を作ることが可能です。 (正確に言うと、新しい関数が定義されます。 ) ∫ {exp^ (x^2)}dx以外には、指数積分∫ { (e^x)/x}dx,対数積分∫ (1/logx)dx, 三角積分∫ { (sinx)/x}dx,∫ { (cosx




微积分学 不定积分 练习答案 维基教科书 自由的教学读本
2:y軸として、exp(x^2)を作る 3:y軸を台形積分するための関数を入力する 4:積分結果がどの程度正しいかを評価する といった順で解説します。 まずは左図のように入力します。 ここでx0とdxはx軸を作るためのパラメータで、x=x0m*dx(mは正の整数)となります。 これから、A列にx軸を作り不定積分の計算(解析学A) (担当:高橋淳也) 1 不定積分の計算 ここでは,不定積分の計算方法を述べる.一般に初等関数の不定積分は初等関数で書けると は限らないが(例えば, ∫ e 2x dxは初等関数で書けない),特別な場合に初等関数で書け るので,その場合について説明する. 以下 · だから、e^(x^2)を積分する代わりにe^(x^2y^2)を積分してその√を取れば解が得られるという論法を利用するんですね。 四角形の領域で I=∫x,y0→ae^(x^2y^2)dxdy を積分するにはちょっとなんで、四角形に接する大小の円で挟み撃ちを考えるんですね。
∫exp(x 2) dx = √(π)/2 ・・・ (2) 積分区間0∞ 図3のように、刻み幅(h)を05としてエクセルを用い数値積分を行った。x=5で台形の面積が極めて小さくなったので累積を中断した。計算結果と解析解は16桁以上一致しており、極めて精度が良いことが解る。 図3 エクセルを用いた台形公式による数値不定積分を計算する: x^5 dxの積分 x^2 sin^3 x の積分 ∫e^t sin (5t) 基本項では表せない不定積分を計算する: e^ (t^2)の積分 1/sqrt (1u^4)を積分する 与えられた関数を含む積分の表を生成する: cos (u)を含む積分 · こんにちは! 今回は、文系出身の方に向けて、大学数学や数学3でよく出てくる"exp"という用語の意味や計算方法について解説していきたいと思います! expについて徹底解説 expの意味 まず、"e"という数学用語が微妙な方のために説明をしておきますね。 eとは、ネイピア数のことです。
09 年度物理数学II 宿題(11 月2 日出題、9 日提出) 解答 担当吉森明 問題1(1) 図のような積分路Cで R C exp−z2dz を計算することでR ∞ −∞ exp−x2cos(2bx)dx を求めよ。(2) 前回演習の問題No4II(c)~(g) をやりなさい。 解答 (1) a) exp−z2 は全複素平面内で正則なので、積分路をC とする積分する関数を入力してください 変数 始点 終点 被積分関数 exp (x^2) を次の変数で微分する x 100から100への間隔で = グラフを描く LaTeXエディタで編集 このページへの直接のリンク 定積分の計算 ある区間で定義された関数の定積分を数値注意 6 15 (不定積分の関数の表現) 不定積分は計算の方法により得られる結果が一見すると 違うときがある. これは不定積分が任意定数の不定性をもつためである. 注意が必用である. 例 6 16 (置換積分の使用例) ここで, とおき, , を用いた. 例 6 17 (置換積分の使用例) 例 6 18 (置換積分の




广义积分 Exp X 2 Dx 从负无穷到正无穷 原函数似乎求不出来啊 怎么算 雨露学习互助
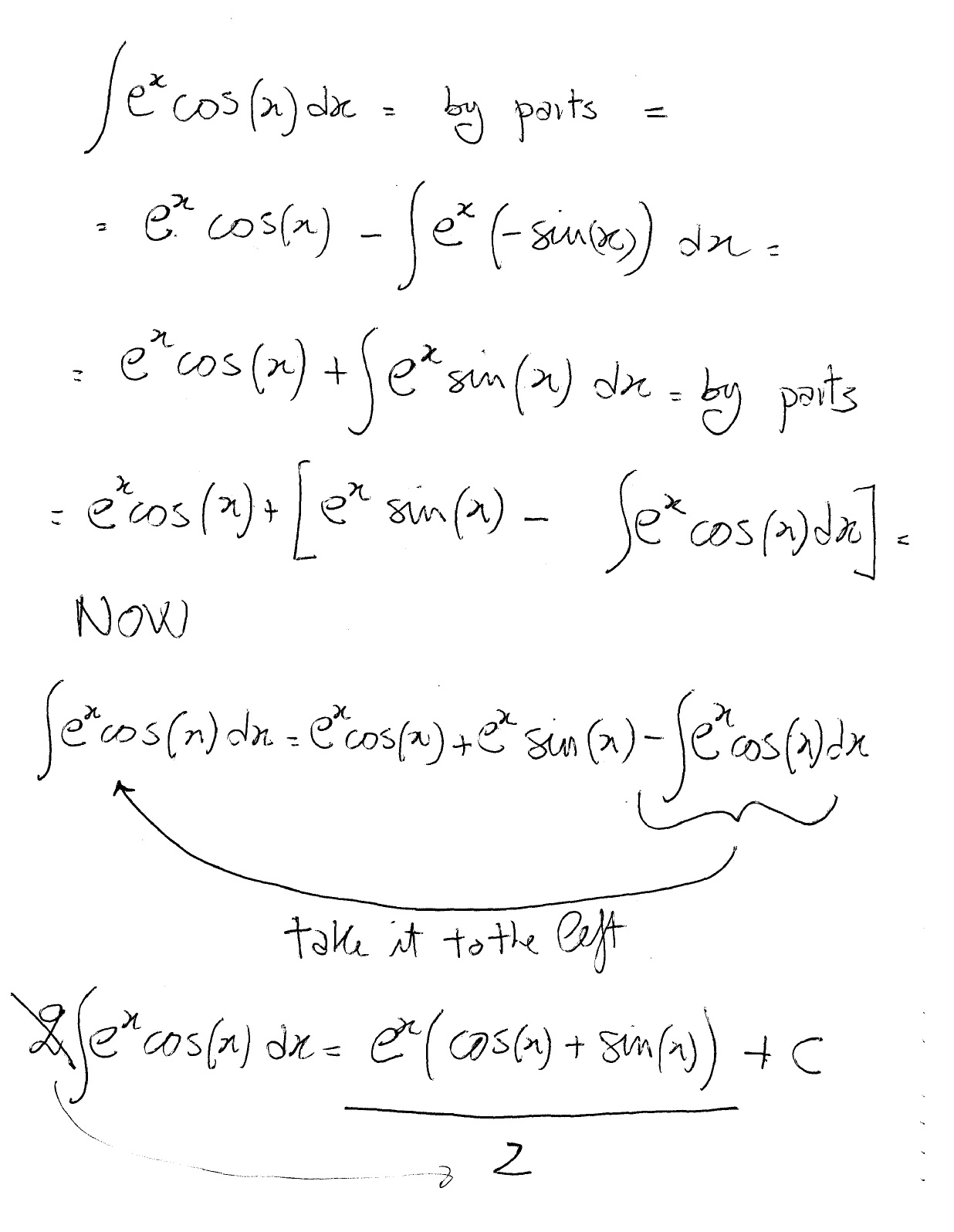



How Do You Find The Integral Of E X Cosx Dx Socratic
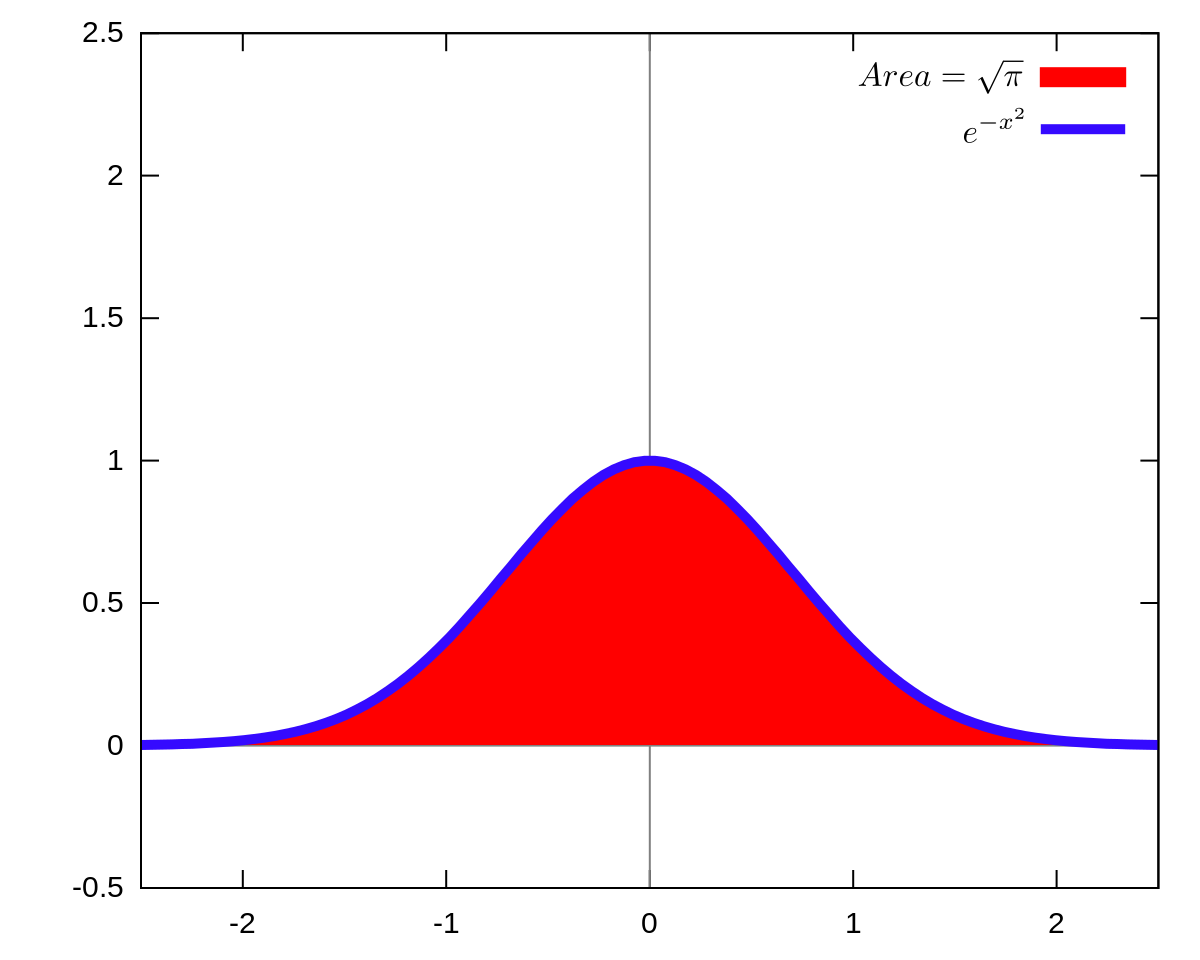
· e^(x^2)の原始関数を初等関数で表すことは出来ません。 高校までの知識では積分できないと言うことです。 積分範囲を0,∞とすれば定積分は計算でき ∫0,∞{exp(x^2)}dx = (√π)/2 となります。 これは大学2年くらいの知識があれば証明できます。Exp (x^2)の∞から∞までの定積分は? ① 1 ② π ③ π^ (1/2) ④ どれでもない 正解 正解は「③ π^ (1/2)」 標準正規分布の確率密度関数の変数変換でもいいですし、座標製麺の2重積分の極座標変換 · exp(x^2)の不定積分や、cos x = hx の解が初等関数で表わせないことが 金子晃:数理系のための基礎と応用微分積分 II サイエンス社 (01) の第8章付録で証明されています。ところでこの中に 補題10αが無理数の時、x^αは第2位の初等超越関数 というのがあるのですが、これはどうして
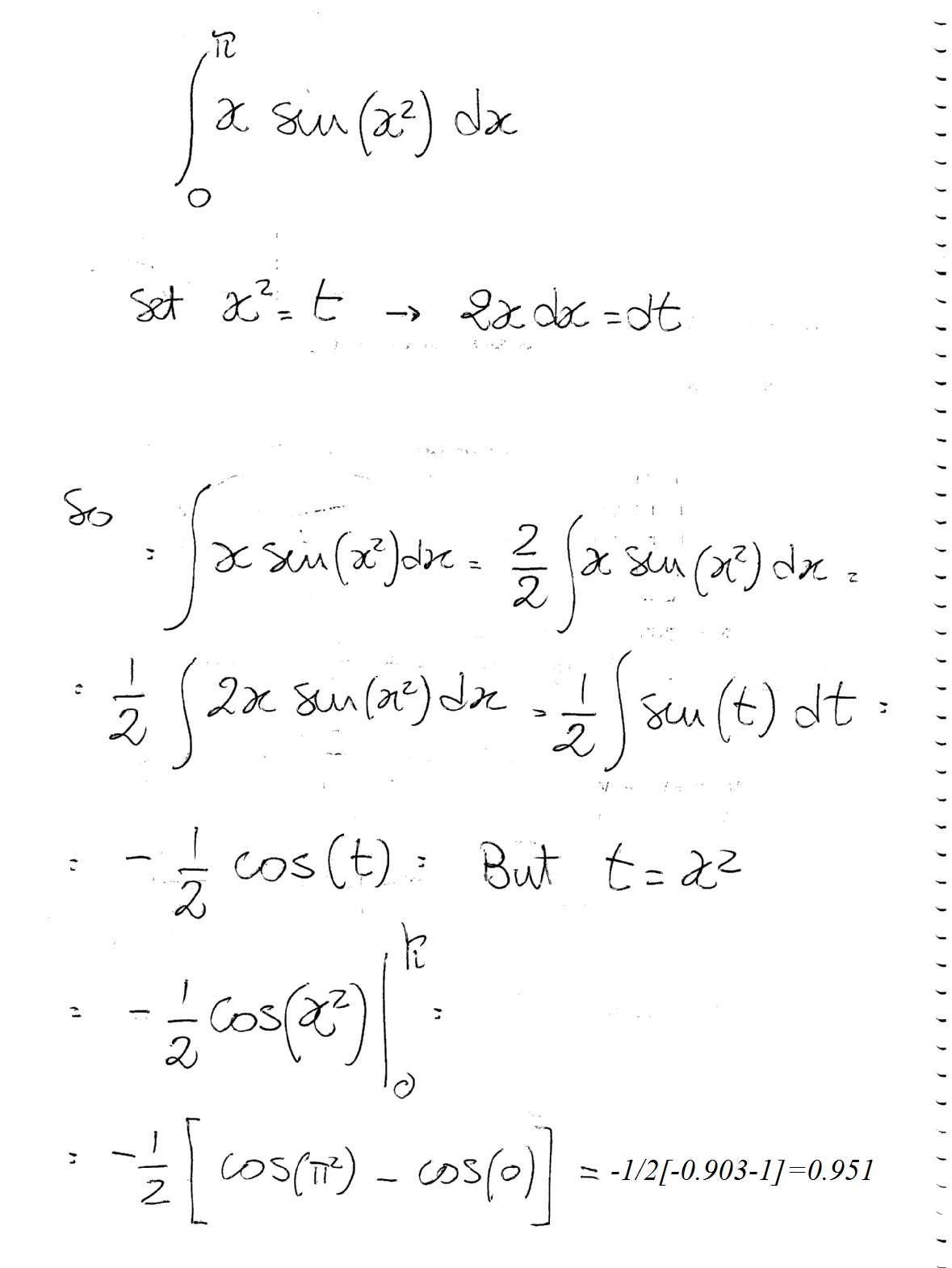



How Do You Use Substitution To Integrate Xsin X 2 Dx From 0 Pi Socratic




What Is The Integral Of 1 1 X 2 Quora
Exp_積分_x^2,積分,積分,積分,積分,exp(ax^2),積分 女性のためのヘアケア、女性用育毛剤・育毛シャンプーに関する話題や情報 このサイトでは、女性用育毛剤・育毛シャンプーなど女性のためのヘアケに関する話題や情報を集めてご紹介しています。ぜひご覧ください。 PR Home >> "exp_積分 · exp {x^2/4abx} u,∞などの定積分 投稿日 年10月19日 年10月19日 投稿者 ぽじぽめ コメントする ただし、全て <証明> 予め、指数部分を平方完成しておきます。 と置きまGauss 関数の積分 21 xe−ax2 の積分 I1 = ∫∞ 0 (1) xe−ax2dx この積分は,次の置換を用いることによって簡単に計算できる。 (2) t= ax2 (3) dt= 2axdx これを式(1) に代入すれば I1 = 1 2a ∫∞ 0 e−tdt= 1 2a (4) 積分範囲が(−∞,∞) であるときは,被積分関数が奇関数なので,積分は
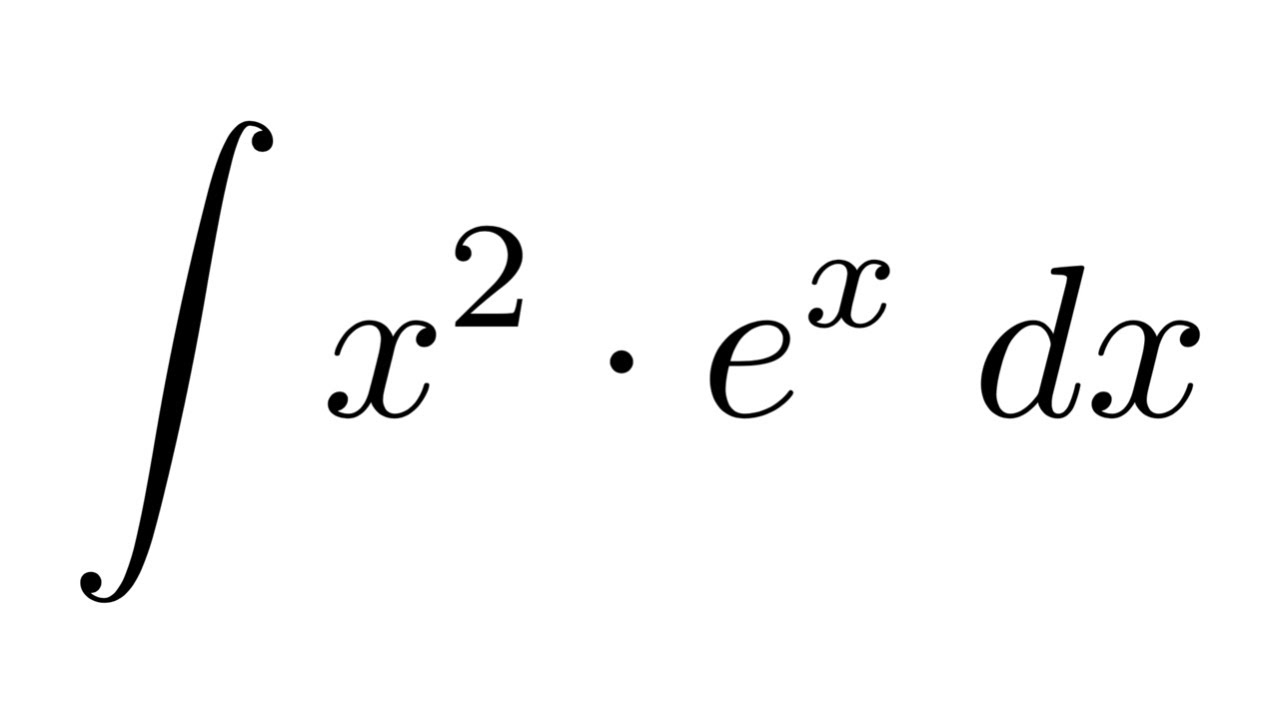



Integral Of X 2 E X By Parts Youtube



求不定积分s Xe X Sqrt E X 2 Dx 数学竞赛平台 数学帮 Math110
1 積分練習問題解答 1 つぎの不定積分を計算せよ。 (1) ∫ x 1 x2 2x5 dx d dx (x2 2x5) = 2(x1)だから x 1 x2 2x5 x1 x2 2x5 2 x2 2x5 と変形して,y = x2 2x5 とおくとdy = 2(x1)dx だから ∫ x1 x2 2x5 dx = ∫ dy 2y = logjyjC = 1 2 log(x2 2x5)C一方,後半の積分はx 22x5 = (x1) 4 なので,y = (x1)/2 と書くと · e − a x 2 e^{ax^2} e − a x 2 は偶関数なので積分値が半分になっています。 ガウス積分で,被積分関数に x x x や x 2 x^2 x 2 をかけたものも見かけます: ∫ 0 ∞ x e − a x 2 d x = 1 2 a \displaystyle\int_0^{\infty}xe^{ax^2}dx=\dfrac{1}{2a} ∫ 0 ∞ x e − a x 2 d x = 2 a 1Gaussian exp(x2)のR上の積分値 ∫∞ −∞ exp(2x)dx = p π の導出法について考える。先ずは同値な積分形に書換えて置こう。 命題1. 次は同値である。 (1) ∫∞ −∞ exp(x2)dx = p π (2) ∫∞ 0 exp(x2)dx = p π 2 (3) ∫∞ 0 e−t 1 p t dt = p π (4) 任意のa > 0に対し ∫∞ −∞ exp(ax2)dx = √ π a (5) 任意のa > 0に
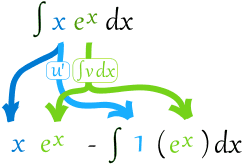



分部积分法
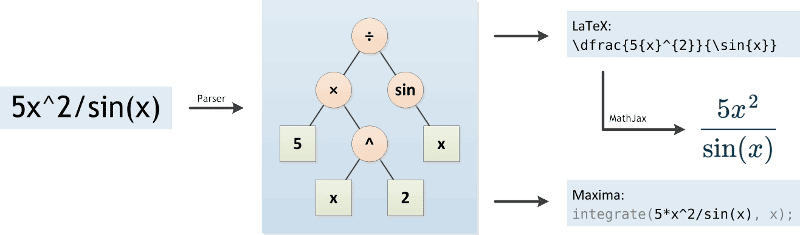



Integral Calculator With Steps
G= x (多項式を積分する側に選ぶのは、 相手が対数のときの例外) ∫wn log x · 1 dx = log x · x − ∫wn 1xn x C=x log x−xC ※ ∫wn(多項式) log xdx, ∫wn(指数関数) log xdx ∫wn(三角関数) log xdx 、などにおいては「 log x を微分する側に選ぶ( g= log x とおく)」とスムーズに計算できる。 逆に選べば( f'= log x とおくと) f すなわち log x の不定積分が必要となり、 x log x−(C は積分定数) 112 n = 2 I2 = Z 1 x2 1 dx = arctanx C (13) (C は積分定数) 113 n = 3 I3 = Z 1 x3 1 dx (14) 11 不定積分 年10 月 日 有理式の定石に則って、分母を因数分解する。 I3 = Z 1 (x 1)(x2 − x 1) dx (15) 部分分数分解をして I3 = 1 3 Z 1 x 1 − x − 2 x2 − x 1 dx = 1 3 lnx 1− 1 3 Z x − 1 2 x − 1 2 2{\displaystyle \int {\frac {e^ {cx}\;dx} {x}}=\ln x\sum _ {i=1}^ {\infty } {\frac { (cx)^ {i}} {i\cdot i!}}}



Http Tyr0 Chem Wsu Edu Kipeters Chem332 Resources Tableofusefulintegrals Pdf




Int E 3x E X E 4x E 2x 1 Dx
· こちらの「具体例で学ぶ数学」さま曰く、mathwordsnet 「平行移動しても定積分の値は変わりません。」(〇ω〇)ぎゃっ↓わての理解 「exp第1項に含まれるダンピング?的な何かは、どちらの教科書でもプリファクターに吸い取らせます的な表現がありますんだ。(%e^(x^2) または exp(x^2) を微分する。) 積分 Maxima では不定積分、定積分が計算できます。 積分定数は表示されないので注意してください。 また、うまく計算できないこともあります。 integrate(f(x), x) 不定積分 integrate(f(x), x, a, b) 区間 a, b の定積分この漸化式をもとに, ∫ x 3 e x d x の積分を計算してみる. I 0 = ∫ x 0 e x d x = ∫ e x d x = e x I 1 = x 1 e x − 1 · I 0 = x e x − e x = (x − 1) e x I 2 = x 2 e x − 2 I 1 = x 2 e x − 2 (x − 1) e x = (x 2 − 2 x 2) e x I 3 = x 3 e x − 3 I 2 = x 3 e x − 3 (x 2 − 2 x 2) e x = (x 3 − 3 x 2 6 x − 6) e x のように, I 0 , I 1 , I 2 , I 3 と順次漸化式を利用して計算するとよい.




X2ex积分 求不定积分 E X 47 X 2 Dx 三人行教育网 Www 3rxing Org




Indefinite Integral Of 1 X Antiderivative Of 1 X Video Khan Academy
Exp(ix^2)のガウス積分 home> 物理数学> このページのPDF版 サイトマップ ファインマンの経路積分で何気なく使っていたので,確かめてみました.短いです. と置きます. すると,収束因子として, を用いて, となり,よって, ですね.なるほど, ですから,この に を代入したものに一致す積分電卓 積分する関数を入力してください 変数 被積分関数 x*exp (x^2) を次の変数で微分する x %e^x^2/2 グラフを描く LaTeXエディタで編集 このページへの直接のリンク 変数に次の値を代入する x= 積分電卓 解析積分を用いて所与の変数に対する関数の不定積分 (アンチ導出)を計算する。 また、関数のグラフとその積分を描画することもできる。 · ガウス積分の漸化式 $ \int x^2 \exp \alpha x^2 \mathrm{d} x$ $ \int x^3 \exp \alpha x^2 \mathrm{d} x$ $ \int x^4 \exp \alpha x^2 \mathrm{d} x$ $ \int \exp (ax^{2} bx c) \mathrm{d} x$ ガウス積分の定義と証明 ガウス分布(正規分布)に対する下記の積分をガウス積分と呼ぶ。 積分範囲が ∞ に及ぶので、正確には広義




微积分学 不定积分 练习答案 维基教科书 自由的教学读本




How To Integrate X 3 E X 2 Using Integration By Parts Youtube
の積分路 C 1 例 42 I = Z 1 0 x sin ax x 2 1 d x (a> 0) (613) sin ax =(e i ax e) = (2i) を用いて書き換える。 I = 1 2i Z 1 0 x x 2 1 (e i ax e)d x 1 e i ax d (614) ここで f (z)= z z 2 1 (615) とおくとジョルダンの補題により図 61 の積分路 C R 上の複素積分 Z C R e i az f (z)d (616) は R!1 の極限で 0 に収束する。これを加えて I物理を学んでいると,頻繁に出てくる積分というのがあります.その一つがガウス積分です. ガウス積分 ガウス積分とは,つぎのような式で書かれる積分のことです. I = ∫ ∞ −∞ e−ax2dx (1) ここでx は実数,a は正の定数です. ガウス積分の公式を部分積分法を使い求めてみよう.f′(x) = ex,g(x) = x とみなすと, f(x) = ex,g′(x) = 1 と考えればよいので, ∫ 2 0 xexdx = xex2 0 ∫ 2 0 exdx = 2e 2 ex 0 = 2e2 e2 1 = e2 1 例52 次に, ∫ logxdx を部分積分法を使い求めよう. ∫ logxdx = ∫ 1 logxdx = ∫ (x)′ logxdx = xlogx ∫ x 1 x dx = xlogx ∫ dx = xlogx xC 計算練習3
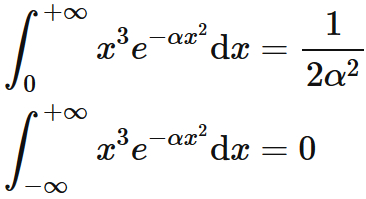



Gaussian Integral Formula And Proof Semath Info




高数之微积分 Dx E X E X 需要详解 雨露学习互助
· 部分積分で次数を減らしてみましょう。 =(x/2)*exp(x^2)∫(1/2)exp(x^2)dx (2x*exp(x^2)=(exp(x^2))')指数関数 \(e^{x^2}\) は正規分布(ガウス分布)の確率密度関数を表わすのに使用されますが,その不定積分 \(\int e^{x^2}dx\) は初等関数では表わせません.しかし,ゼロから無限大まで積分すると \(\frac{\sqrt{\pi}}{2}\) になることは次のようにして導きます (数学的には厳密ではないかも知れません)以下是部分指數函數的積分表 ∫ e c x d x x = ln x ∑ i = 1 ∞ ( c x ) i i ⋅ i !



求不定积分s Xe X E X 1 2 Dx 数学竞赛平台 数学帮 Math110
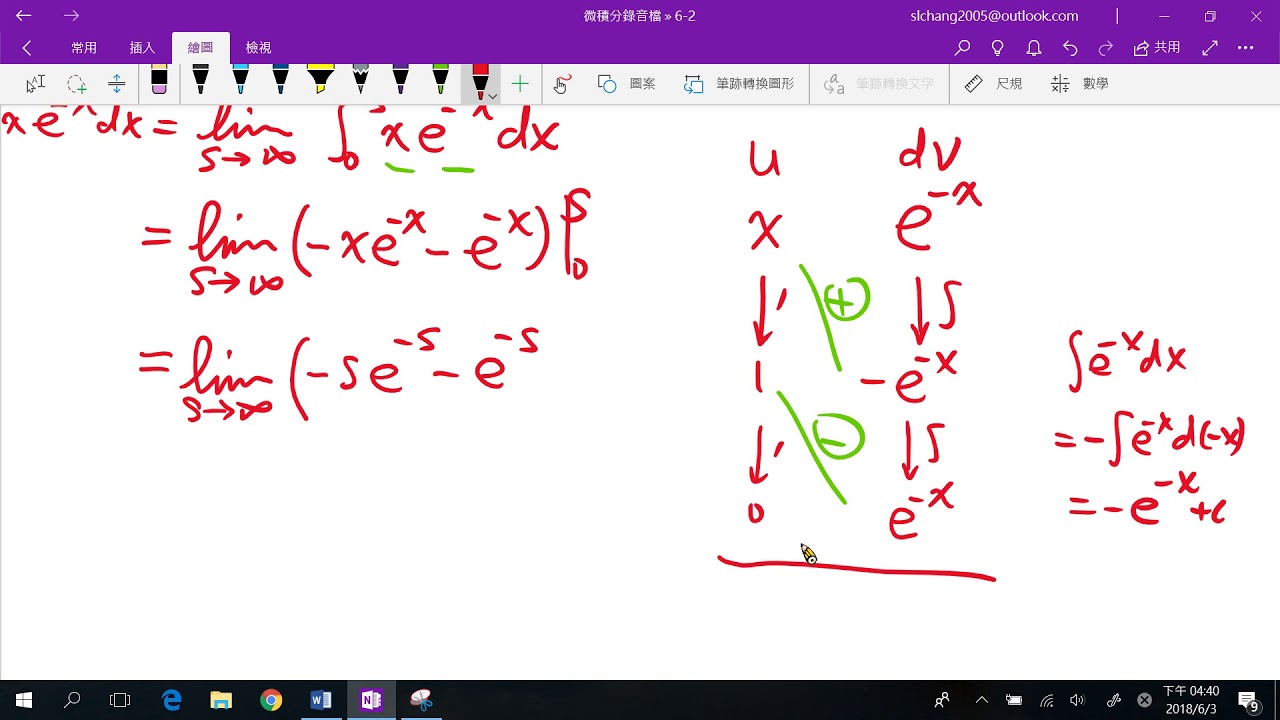



6 2 5 3 瑕積分int 0 Infty Xe X Dx Youtube
定積分 這樣的極限 在我們討論f 函數曲線下的面積,或者討論給定速度的情況 區間長度為 x = (2 –1)/5 = 利用中點法估計得 27 範例五/ 解 ≈ 中點法計算的黎曼和即右圖的 長方塊面積。 圗十一 cont'd 28 定積分的性質 29 定積分的性質 我們定義定積分時,我們預設定積分 的上、下 界a, b
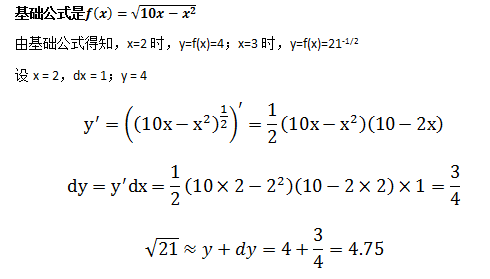



单变量微积分笔记11 微分和不定积分 我是8位的 博客园



以下计算积分 X E X 2 Dx 的过程错在何处 知乎



计算二重积分ss D E X 2dxdy 其中区域d是第一象限中由曲线y X 3及曲线y X所围成的区域数学竞赛平台
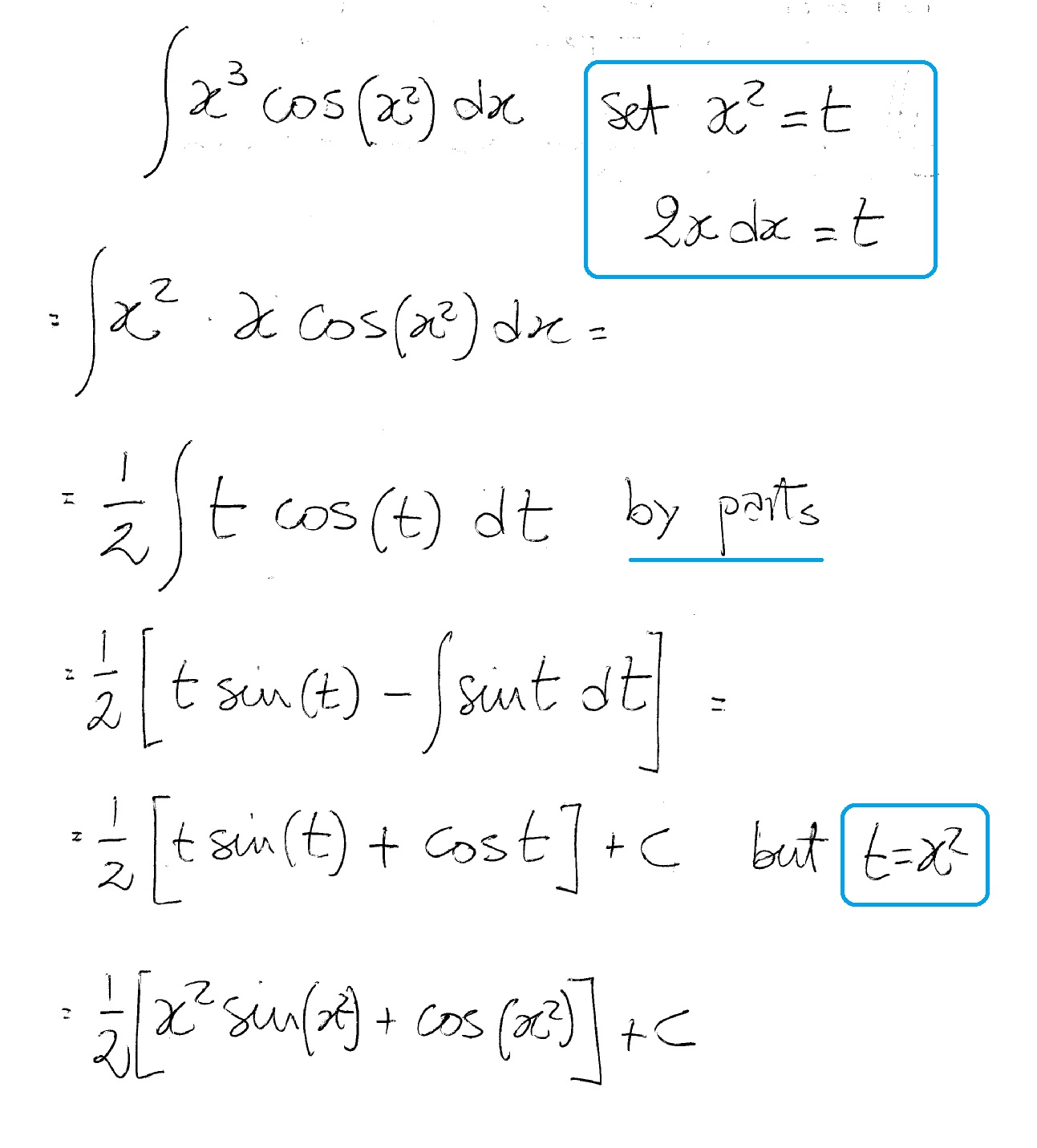



How Do You Integrate X 3cos X 2 Dx Socratic



从 E X Sinxdx出发 积分随想 I 知乎



Search Q E E7 8d E5 86 Tbm Isch




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2



从 E X Sinxdx出发 积分随想 I 知乎




定積分 Int Frac 1 1 E X Dx



E 2x 積分 達人專欄 Uvyo




一道高数题设 A 1 求积分f A X A E X Dx的最大值那个其中是e的x次方我不知怎么打 雨露学习互助
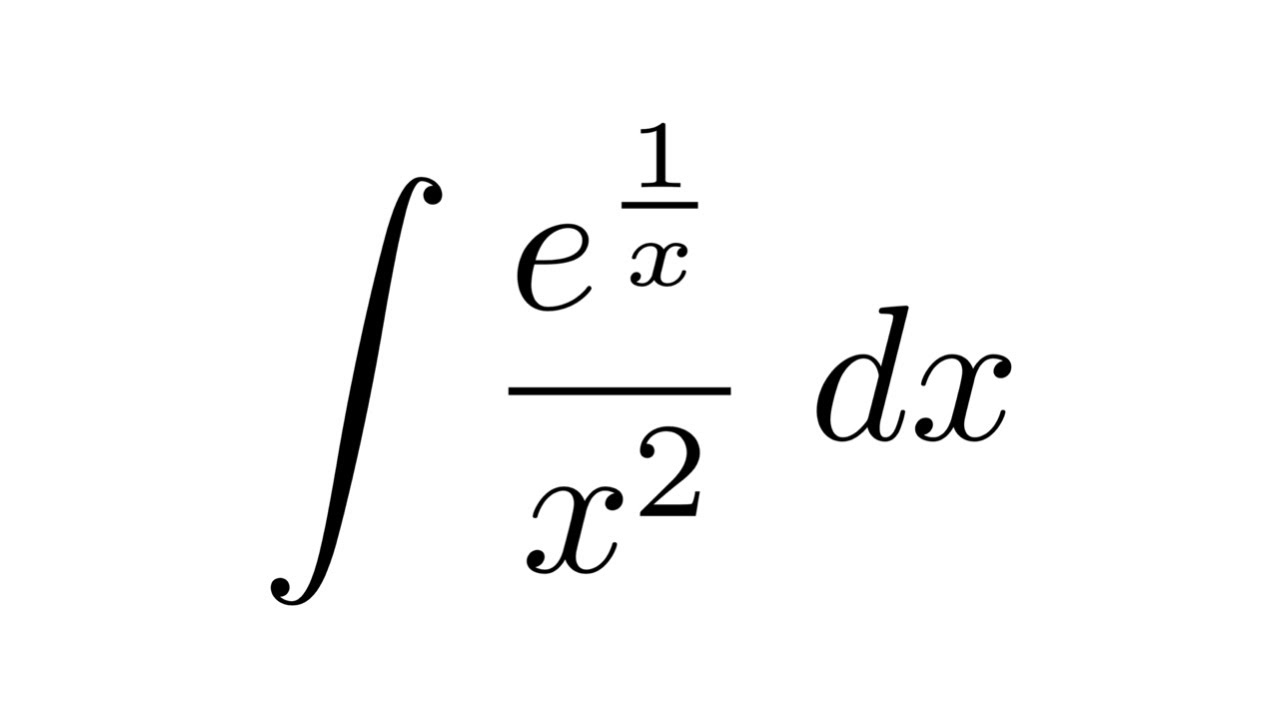



Integral Of E 1 X X 2 Substitution Youtube




E的负x平方的积分 在线图书馆
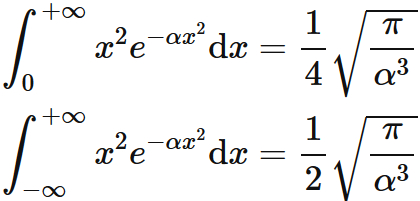



Gaussian Integral Formula And Proof Semath Info



1



Search Q E 2 E7 8d E5 86 Tbm Isch




Dirichlet Integral Wikipedia
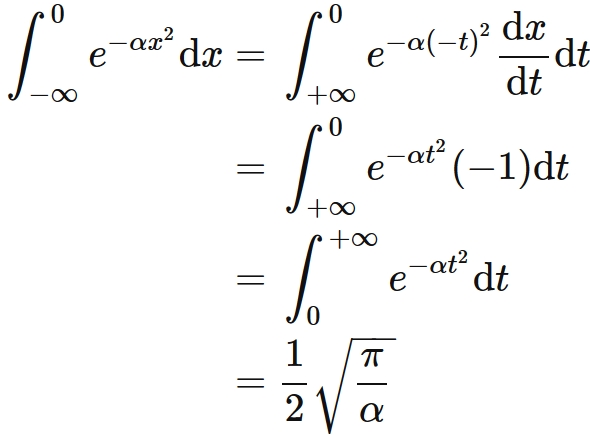



Gaussian Integral Formula And Proof Semath Info




求无穷积分 求e X 0到正无穷的积分 三人行教育网 Www 3rxing Org
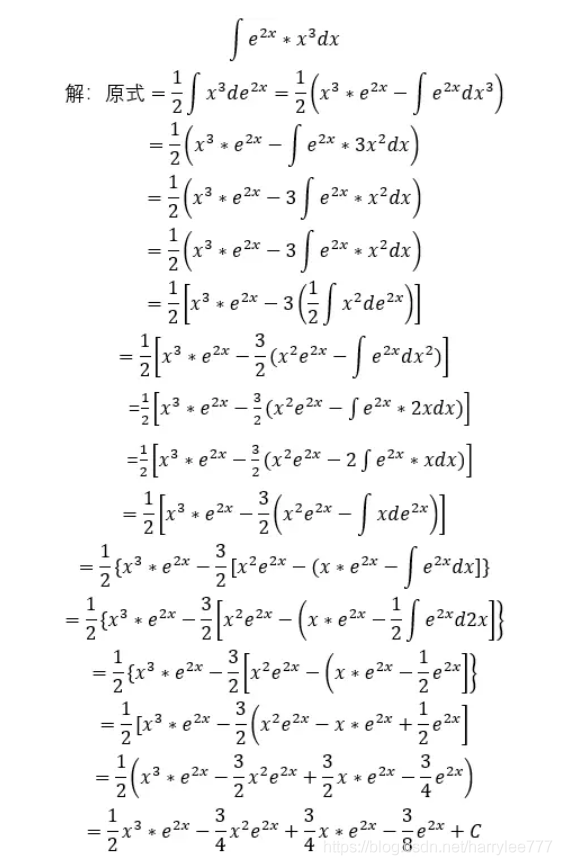



表格 列表法之分部积分 Harrylee777的博客 Csdn博客 表格法求分部积分




Gaussian Integral Wikipedia
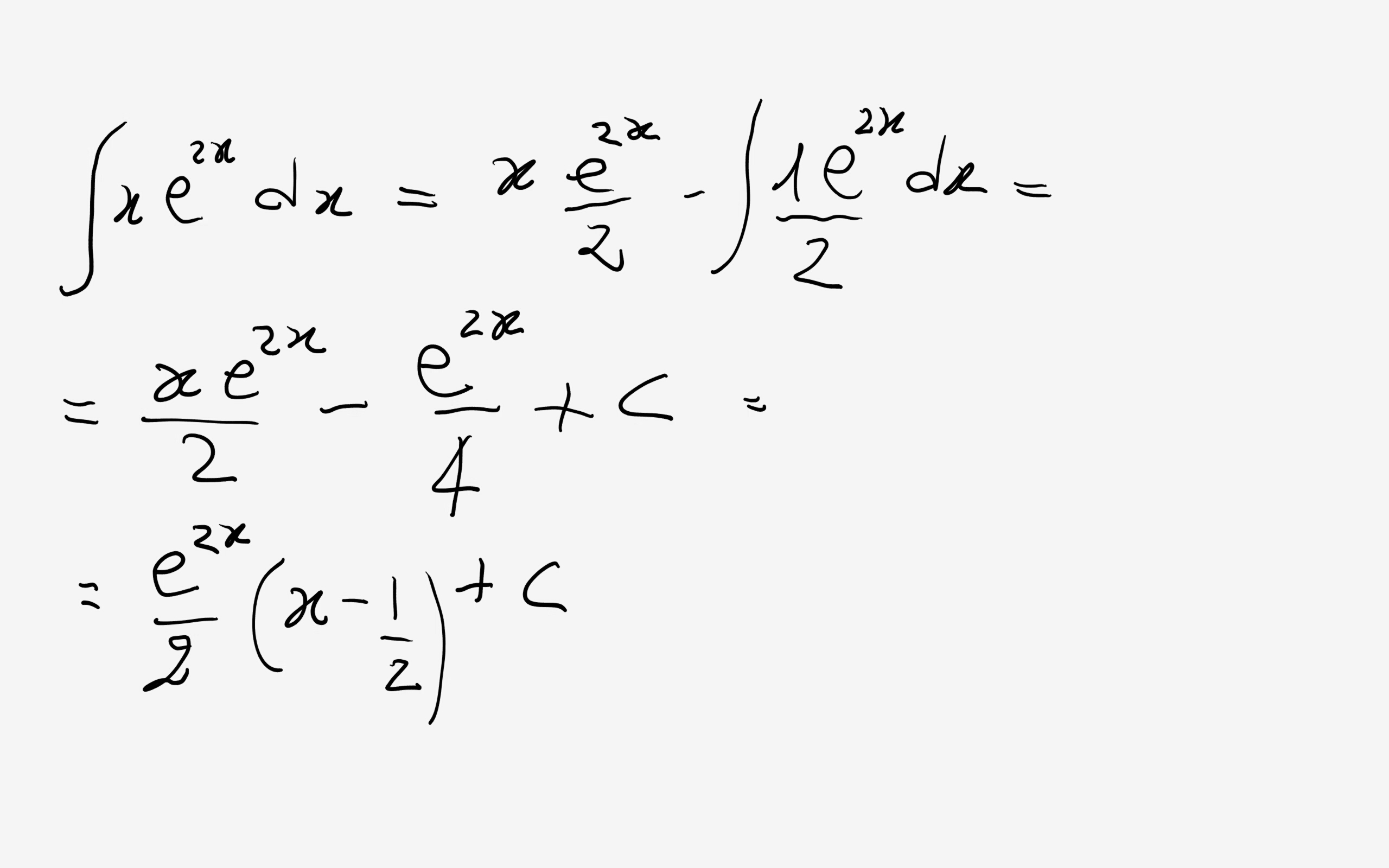



How Do You Integrate Xe 2x Dx Socratic



1




Int E 3x E X E 4x E 2x 1 Dx



E的x次方积分 万图壁纸网



E X 2 Dx的三种方法 知乎
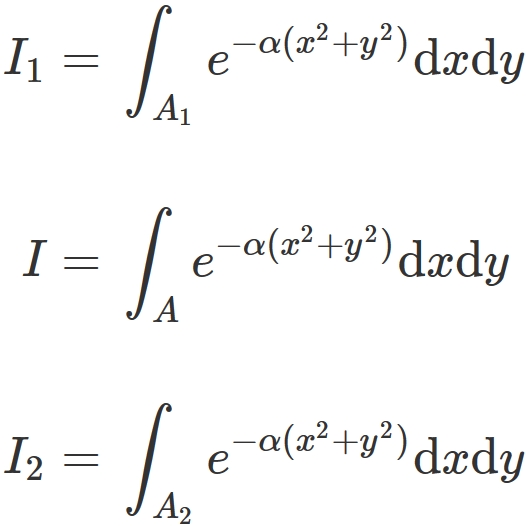



Gaussian Integral Formula And Proof Semath Info
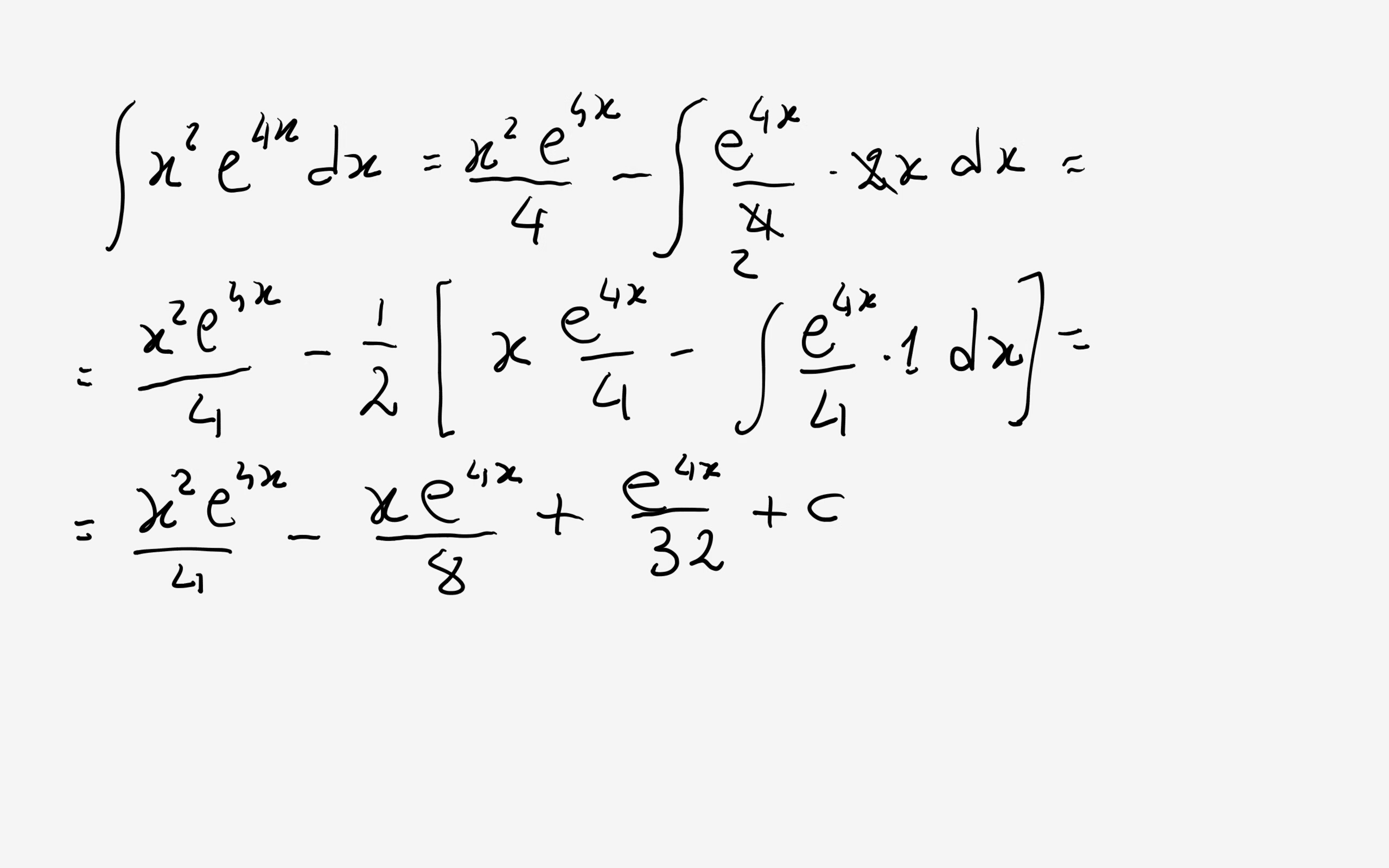



How Do You Integrate X 2 E 4x Dx Socratic




如何计算e的 X的平方 次方的不定积分 知乎




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2



X 2 E 2x的积分怎么求 数学作业 解题作业帮




X 2 E X 2 X 2 Dx用于积分 365结算错误我又投注了 365bet平台赌场




Gaussian Integral Wikipedia




What Is The Integration Of 1 Xe X Quora



以下计算积分 X E X 2 Dx 的过程错在何处 知乎



估计积分的值 4 S 0 2 E X 2 X Dx 数学竞赛平台 数学帮 Math110




E的x次方积分 在线图书馆




X找到积分 Ex 2找到积分 积分x的结果会怎样 365最新备用网址 Bet365手机客户端首页




ガウス積分の公式集 証明付 理数アラカルト



置換積分でexp X 2 の積分を求めたいのですが T X 2としてもt Yahoo 知恵袋




Ex 7 6 21 Integrate E 2x Sin X Using Integration By Parts



急求数学帝解答exp X 1 Exp 2x 积分过程我知道答案是atan 1 Exp X 1 Exp X 但是自己积分怎么就积分 不出来呢 我是令t Exp X 然后化成1 T 2 1 1 T 2 积分 但是这样的结果是 Exp 1 Arctan Exp X 作业 慧海网




Integration By Parts Wikipedia
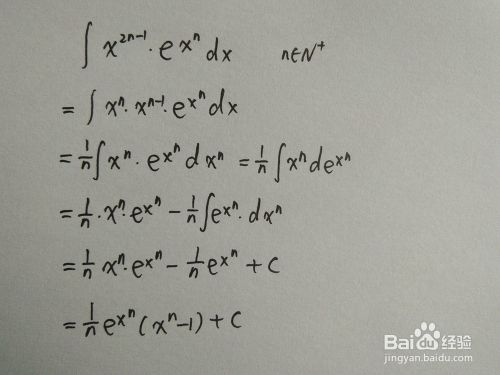



如何求形如 X 2n 1 E X N Dx的不定积分 百度经验



Http Tyr0 Chem Wsu Edu Kipeters Chem332 Resources Tableofusefulintegrals Pdf



What Is The Integral Of E F X Quora




求不定积分 1 二次根号下 E的x次方加二 雨露学习互助




ガウス積分の公式集 証明付 理数アラカルト




微积分学 不定积分 练习答案 维基教科书 自由的教学读本




E的x次方定积分x乘以e的负x次方 定积分




求不定积分xe X 1 X 2 Dx 雨露学习互助




实验十用mathematica计算重积分



从 E X Sinxdx出发 积分随想 I 知乎



单变量微积分笔记11 微分和不定积分 我是8位的 博客园



不定积分的解题思路及技巧总结 知乎




ガウス積分




高斯积分 维基百科 自由的百科全书
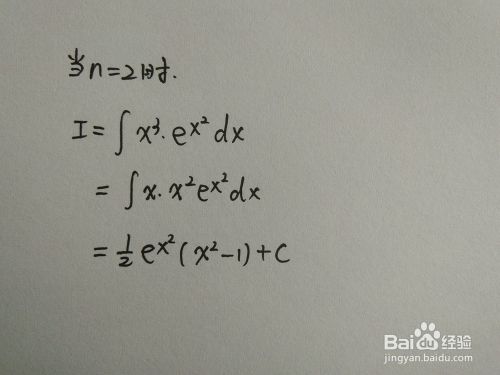



如何求形如 X 2n 1 E X N Dx的不定积分 百度经验
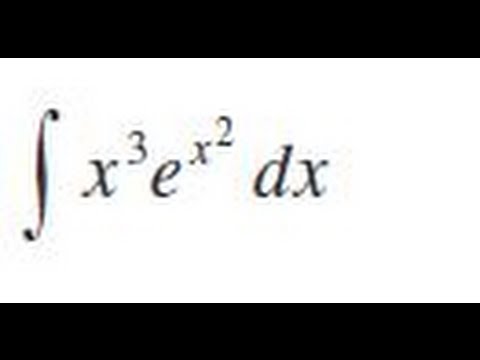



Integrate X 3 E X 2 Dx Youtube



计算二重积分ss D E X 2 Y 2 N Sin X 2 Y 2 Dxdy 其中积分域d X Y X 2 Y 2 P 数学竞赛平台 数学帮 Math110




无穷积分求 E X 2 在0到正无穷的积分求过程 三人行教育网 Www 3rxing Org



Gaussian Integral Wikipedia
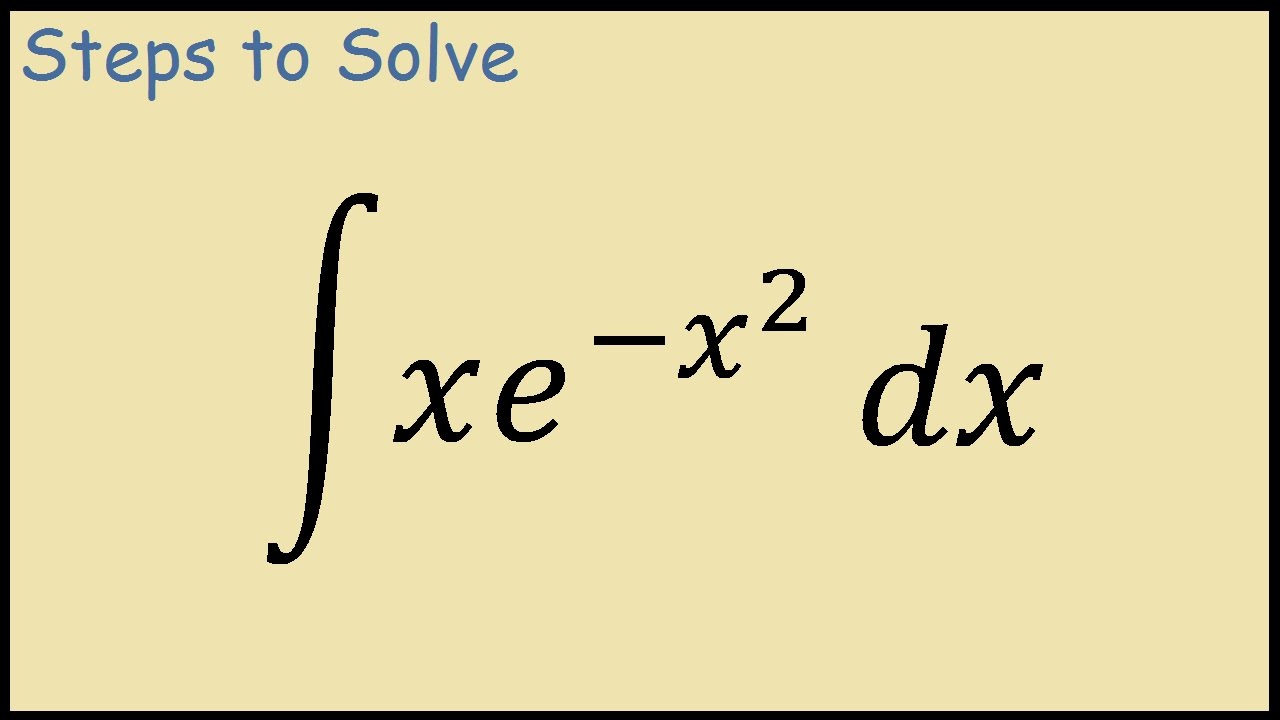



How To Integrate Xe X 2 Youtube




Matlab 在教学中的应用 Ppt Download
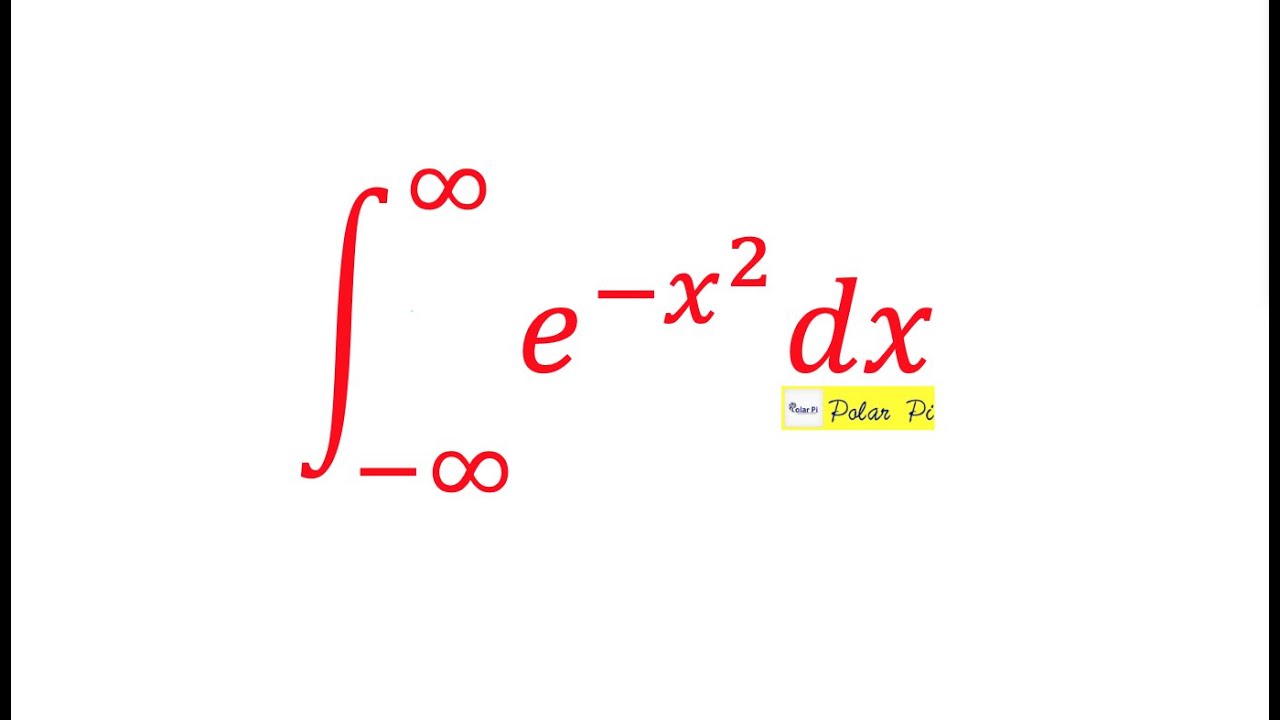



Integral Of Exp X 2 Gaussian Integral Trick Youtube
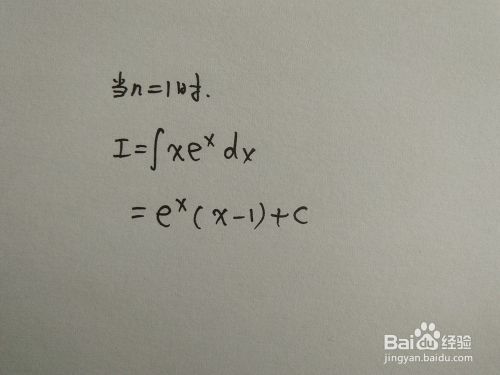



如何求形如 X 2n 1 E X N Dx的不定积分 百度经验




既有e X又有sinx或cosx的积分题的解法 Weixin 的博客 Csdn博客



估计下列各积分值 4 S 0 2 E X 2 X Dx 数学竞赛平台 数学帮 Math110




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C



从 E X Sinxdx出发 积分随想 I 知乎




Integrating E X 2 The Gaussian Integral Youtube




Ex 7 6 21 Integrate E 2x Sin X Using Integration By Parts




Gaussian Integral Wikipedia




高斯积分 积分e X 2 从负无穷到正无穷 哔哩哔哩 Bilibili




Gaussian Integral Wikipedia




超越函数e X 2 的定积分 Norstc的博客 Csdn博客



标签高斯积分下的文章 Joyful Physics




Sym Py Edu



Dp0advswdfuxrm
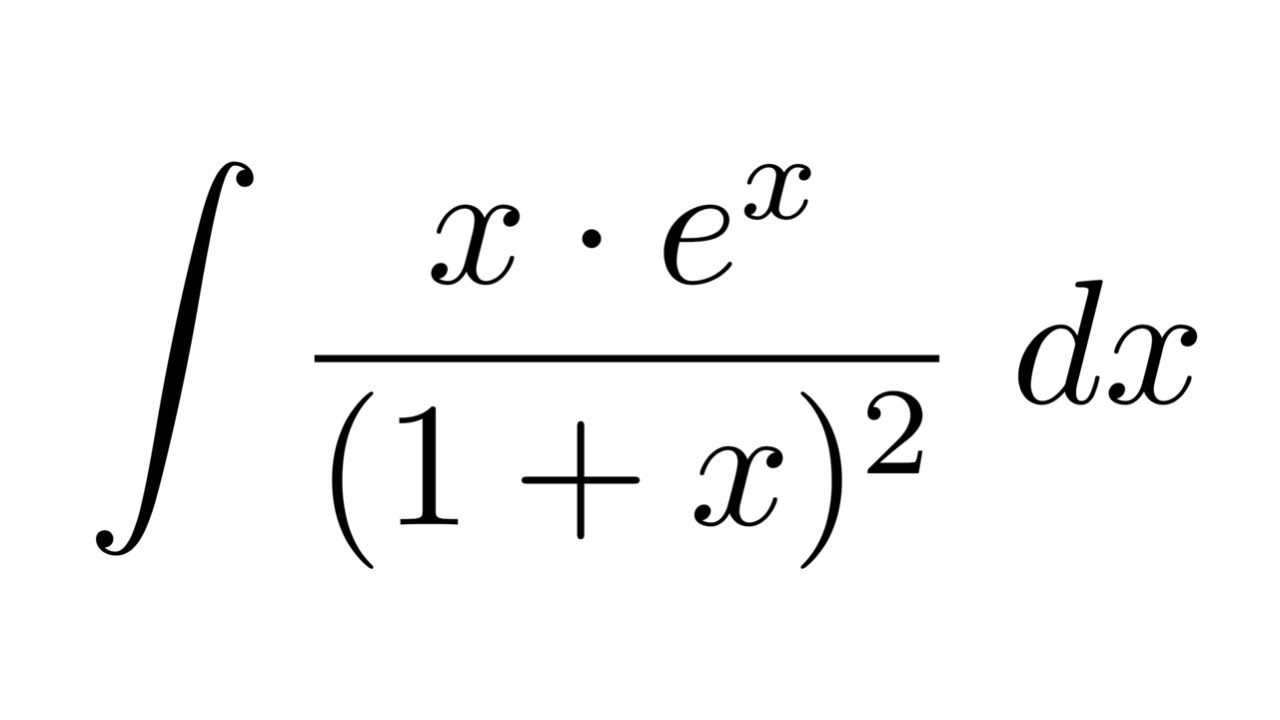



Integral Of X E X 1 X 2 By Parts Youtube



How To Integrate X Sqrt X 2 Y 2 With An Order Dxdy Quora




積分 1 Sqrt E X 1 Youtube




Evaluate Int E X X 3 X 1 1 X 2 3 2 Dx




高斯积分 维基百科 自由的百科全书


コメント
コメントを投稿